نظرية فيثاغورس

 

 المتباينات ونظم المعادلات
الهندسة التحليلية

 

 هندسة المجسمات

نظرية فيثاغورس

 العلاقة بين أضلاع مثلث قائم الزاوية:
 " في المثلث القائم الزاوية مربع الوتر يساوي مجموع مربعي طولي الضلعين الآخرين"
وينقسم هذا الموضوع إلى قسمين:
رمز نقطي  أولاً : إيجاد طول ضلع مثلث قائم بمعلومية ضلعين
فكرة الحل:
رمز نقطي   إذا كان المجهول الوتر .... نربع الضلعين الآخرين ونجمع. " مثال 1 "
رمز نقطي إذا كان المجهول أحد ضلعي القائمة .... نربع الوتر ونطرح منه مربع الضلع الآخر" مثال 2 "
رمز نقطي مثال 1
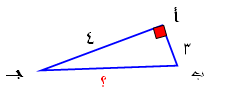
 على الشكل المجاور أوجد طول الضلع المفقود
 الحل:-
 | ج ب| 2 = |أب|2+|أج|2
 | ج ب| 2= ( 3 )2 + ( 4 )2
 | ج ب| 2= 9 + 16
 | ج ب| 2= 25   " بأخذ الجذر التربيعي للطرفين
 | ج ب| = 5

 

  مثال 2

 على الشكل المجاور أوجد طول الضلع المفقود
 الحل:-
 | م ن| 2 = |م هـ |2+|ن هـ |2
 ( 10 ) 2= ( 8 )2   + |ن هـ |2
  100=  64 + |ن هـ |2
  100- 64 = |ن هـ |2
    36  = |ن هـ |2 " بأخذ الجذر التربيعي للطرفين "
    |ن هـ | = 6

تدريب 1: أ ب ج مثلث قائم الزاوية في أ إذا كان | أ ب |= 5 سم ، |أج|= 12  سم  فإن | ب ج |=

17 سم 169 سم 13 سم 34سم


تدريب 2 : س ص ع مثلث قائم الزاوية في س إذا كان | ع ص | = 15 سم ،| س ع | = 12 سم فإن | س ص | =

9 سم 27 سم  81 سم - 9 سم


انياً        ثنانياً : الحكم على أطوال أضلاع مثلث إن كانت تمثل مثلث قائم أم لا " عكس نظرية فيثاغورس "
فكرة الحل :
1-  نكون جدول
2-  نأخذ الضلع الأكبر بعد التربيع
3-  نجمع الضلعين الآخرين بعد التربيع
4-  إذا تساوي الناتجين في  2 ، 3   كان المثلث قائم الزاوية  وإذا لم يتساوى الناتجين كان المثلث ليس قائم

   ( 1 ) الأعداد التالية تمثل أطوال أضلاع مثلث ، أي من المثلثات يكون قائم الزاوية؟
     

  7 ، 8 ، 9      5 ، 12 ، 13 2 ، 7 ، 8 12 ، 20 ، 16

   نكون جدول للفقرة الأولى إذا حققت الشرط فتمثل أطوال أضلاع مثلث قائم الزاوية
العدد 7 8 9
مربع العدد 49 64 81

   نلاحظ ان          81 ≠ 49 + 64

   نكون جدول للفقرة الثانية إذا حققت الشرط فتمثل أطوال أضلاع مثلث قائم الزاوية

العدد 5 12 13
مربع العدد 25 144 169

   نلاحظ ان          169 = 25 + 144 ألأطول تمثل أطوال مثلث  قائم الزاوية

  الأطوال في أنواع خاصة من المثلثات القائمة الزاوية  
       في المثلث ا لقائم الزاوية والمتطابق الضلعين يكون
     
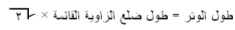
    تدريب :-
طول ضلع الزاوية القائمة نصف طول ضلع الزاوية القائمة  
 
 2- على الشكل المجاور : س = 
 
9سم 18سم

  ملاحظة :- مراجعة مثال 1 في الكتاب ص15


 
    حساب أطوال أضلاع مثلث ثلاثيني ستيني
      


 		  
 تدريب :-  في نصف [ متطابق الأضلاع إذا كان طول الضلع المواجهة للزاوية 530 = 4
 أ)  فيكون طول الوتر=
8 4 2 2 !3
 ب) ويكون طول الضلع المواجهة للزاوية 560 =
2 !3 16 4 !3 4 !2
   المضلعات في دائرة  

1-   طول ضلع مثلث متطابق الأضلاع مرسوم داخل دائرة = نق ×  !3
2-    طول ضلع سداسي منتظم مرسوم داخل دائرة = طول نصف القطر
3-   طول ضلع مربع مرسوم داخل دائرة = نق × !2  
 والعكس :-

ملاحظه :- في حالة إيجاد طول الضلع نضرب وفي حالة إيجاد طول نصف القطر نقسم

 تدريب :-

الحل :-
 إذا كان أ ب جـ  مثلث متطابق الإضلاع مرسوم داخل دائرة (  م ، ) فإن طول ضلع هذا المثلث =
9 سم 3  سم 15 سم

مثلث متطابق الإضلاع مرسوم داخل دائرة (  م ،   =  ) طول ضلعه فيكون طول =
27 سم 9 سم 15 سم
 أكمل الفراغ في نصف المثلث المتطابق الأضلاع ، إذا كان طول الضلع المواجه للزاوية 560 =   5   فإن :
الوتر الضلع المواجه للزاوية 530 الضلع المواجه للزاوية 560
  ...............    ..................

 5