مادة الرياضيات

 

س 1 : - مفكـــــــــوك ( س + 5 )2 =
 أ) س2 + 25           ب) س2 + 5 س + 25            ج) س2 + 10 س + 25         د) 11س2 + 25    

 
س 3 : ( 2 ص – 3 أ )3 = 8 ص3 – 36 ص2 أ +  ...................... – 27 أ3  .   الحد المفقود هو :           

 أ)  18ص أ2                  ب) 54 ص أ            ج) 54 ص2 أ              د) 54 ص أ2             

س 4 : ( أ – 5ب ) ( أ + 5ب )  =  أ2 –  ...................  .     الحد المفقود هو :
 أ) 25ب                    ب) 5ب2                        ج) 25ب2                     د) جميع ما ذكر صحيح .  

س 5 : التحليل الصحيح للعبارة س2 – س – 2 هو :

 أ) (س – 2) (س – 1)     ب) ( س + 2)( س + 1)       ج) (س + 2)(س- 1)        د) (س- 2)(س+1) .   

س 6 : التحليل الصحيح للعبارة    64س2 – 81  هو :

 أ)(8 س – 9)(8 س + 9)   ب)(س – 9)(س + 9)    ج)(8 س – 9)(8 س– 9 )    د)(8 س– 3)(8 س+ 3)  

س 7 : التحليل الصحيح للعبارة     س3 +2 س2 – 3س – 6  هو :

 أ) (س2 + 3) (س + 2)     ب) (س2 – 3)( س + 2)      ج) (س2 + 2)(س– 3)     د) (س2– 3)(س– 2)

س 8 : التحليل الصحيح للعبارة 2 س + 3 س2 هو :

 أ)  س( 2 – 3س)             ب) 5س( 2 +3س)           ج) س( 2 س2 +3 س3)      د) س( 2 +3س)                   

س 9 : التحليل الصحيح للعبارة     أ ( س – ص ) –  ب ( ص – س )   هو :

أ) (س – ص) ( أ – ب)     ب) ( س + ص)( أ – ب)     ج) (س – ص)( أ + ب)     د) (س+ ص)( أ + ب)

س 10 :   س2 +9 س – 10 = ( س + 10 ) ( ..................... ) .      العامل المفقود هو : 

  أ) س + 1                   ب) س – 1                          ج) س + 9                    د) س – 9  .            
 

س 11 :   س2 – 7 س + 12 = ( س – 3 ) ( ..................... ) .      العامل المفقود هو : 

  أ) 4 – س                    ب) س + 4                       ج) س– 4                د) جميع ما ذكر صحيح  .    

س 12 :  أي من العبارات الرياضيــــــة التالية تُمثل عبارة كســـرية  : ( حيث : ص ¹  0 ) . 

  أ)  1 + ب                    ب)   س + أ                       ج)     – ب              د) جميع ما ذكر صحيح 

      5                                 13                                ص + 1

              

 

س 13 : بسّط العبارات الكسرية التالية :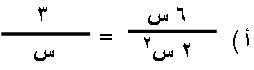
          

 

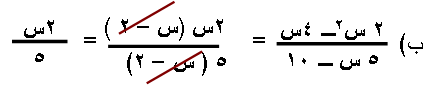س 14 : أوجد الناتج في أبســــط صورة  :

 

س 15 أوجد الناتج في أبسط صورة :-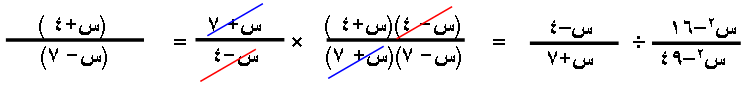

 

س 16 : أوجــد مجموعة حل المعادلات التالية في ح   :

 أ ) س ( س – 6 ) = 0
   س = 0 أو س = 6
   ع= { 0 ، 6 }





 		  ب )  س2 – 18 = 0 بضرب الطرفين×2
       2

س2 – 36 = 0  بإضافة + 36 للطرفين
   س2 = 36   بإخذ الجذر التربيعي للطرفين
   س = ± 6 
   ع= { +6 ،- 6}   
 

 ج) س2 – 49 = 0
 س2 – 49 = 0  بإضافة + 49 للطرفين
 س2 = 49   بإخذ الجذر التربيعي للطرفين
 س = ± 7
  ع= { +7 ،- 7}
 


 

 

 د ) س2 + 7 س + 6 = 0
يمكن حل هذه المسألة باستخدام طريقة المقص أو الحالة العامة                                 

 ( س +6 ) ( س + 1 ) = 0
 س = - 6   &  س = - 1
ع= { -6 ، -1 }
 

هـ )  4 س2 – 15س + 9 = 0
 ( 4س – 3) ( س – 3 ) = 0

 أما 4س- 3 = 0 ← 4س = 3  ← س = ¾
 أو س – 3 = 0  ← س = 3

 ع= { ¾، 3 }

 

 

س 17 : أكمــل ما يلي إلى مربع كامل  :

  أ ) س2 + 10 س     الحــل :  معامل س = 10 ، نصف معامل س = 5 ، مربع نصف معامل س = 25
     س2 + 10 س  + 25 = ( س + 5 ) 2   
 ب) س2+ 4  س     الحــل :  معامل س = 4/5  ، نصف معامل س 4/5 ÷ 2 = 4/5 × 1/2 = 2/5 ، مربع نصف معامل س = 4/25
             5  
     س2+ 4/5  س + 4/25 = ( س + 2/5 ) 2    
 ج)  س2 – 18 س   الحــل : س2 – 18 س  + 81 = ( س - 9 ) 2
          

 

س 18 : حـــل المعادلات التاليــــــة بإكمــال المربع :-

أ )  س2 – 6 س + 7 = 0  الحل :-

   س2 – 6 س  = - 7      

س2 – 6 س + 9 = - 7 +9     " بإضافة مربع نصف معامل س إلى الطرفين"
   ( س – 3 )2 = 2
 

   ( س – 3 ) = ±      
  وهو المطلوب